原创 郭瑞东 集智俱乐部 收录于话题#复杂科学前沿202035个
侦探小说中,神探们能从一堆看似杂乱无章的事件或物证中,抽丝剥茧地发现真相,即案件背后有序的因果链条,在中黄碧薇博士的关于因果发现的分享中,讲述了如何用算法,做复杂系统中的“福尔摩斯”。
黄碧薇是美国CMU在读博士,其所在研究组开发的因果关系自动发现智能平台Tetrad获2020世界人工智能大会SAIL奖,相关网址:
自9月20日(周日)开始,集智俱乐部还将举行一系列有关因果推理的读书会,欢迎更多的有兴趣的同学和相关研究者参加,一起迎接因果科学的新时代。该文的作者黄碧薇也会在读书会期间再详细具体深入的介绍因果发现这个主题,系列读书会详情与参与方式见文末。
1. 何谓因果发现
因果推断中,通常假设因果图是已知的,即我们知道变量之间可能存在怎样的因果关系,只是需要通过自然实验或观察数据,来判断因果关系是否成立。
例如某人声称穷人吸烟多,而穷人患肺癌的比例更高,而这意味着“吸烟多的人患肺癌多”不能支持“吸烟引起肺癌”,这就是一个已知的因果链条。然而真实世界中,类似的因果链条,往往并不是先验知识。
寻找因果关系,传统的方法是通过随机对照实验。但是这种实验方式在实际问题中可能涉及到一些伦理问题,并且通常需要花费大量的人力和物力。因此我们希望寻找一个更切实可行的方法:这就是我们接下来要谈的因果发现,即从观测数据中发现因果关系。相对来说,观测数据是更容易获取的,特别是在大数据时代。
因果发现不同于找到数据间的依赖关系,如果通过观察,发现变量A的值不同时,变量B的分布也不同,那么这两个变量之间就存在依赖关系(相关性)。但只有在变量A能“主动”不同的选择后,变量B的分布发生改变,才能说变量A和B之间存在因果关系。
在因果发现中,很多时候不能简单地根据事件的发生顺序,确定因果关系。例如气压计的水银柱下降和下雨概率增加相关,并且水银柱的下降要早于下雨,但是事实是两者之间并不存在因果关系,他们之间的相关性是由于大气压降低同时造成了水银柱的下降和下雨。而且很多数据可能不包含时序信息,比如独立同分布的静态数据。
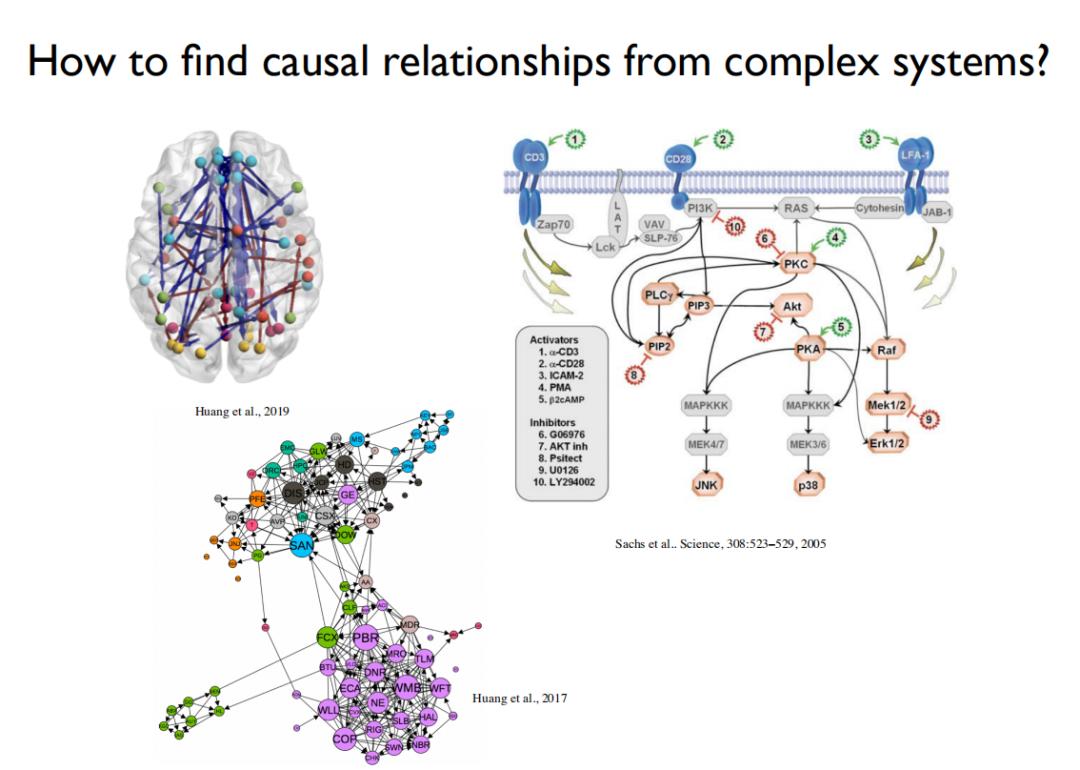
上图列出了因果发现的三个应用场景,分别是:(1)基于大脑影像时序数据,找出不同脑区之间的因果图;(2)基于细胞内的蛋白质浓度变化,推测基因调控网络;(3)根据金融市场的交易数据,推测不同行业的股票价格之间存在的因果关系。
上述三个例子都来自复杂系统,由于涉及的变量很多,如果通过传统的随机对照实验进行验证,所需做的实验数量是超指数增长的,在现实中是不可接受的。
2. 因果发现算法及其假设
下面简要介绍基于条件约束 (constraint-based) 的因果发现算法和基于功能因果模型 (functional causal model-based) 的因果发现算法。
通过马尔可夫条件和faithfulness假说,可以在因果图结构和统计独立性之间建立一个对应关系。特别是在无环图的情况下,这种映射是一对一的。因此我们可以通过判定观测变量之间的条件独立性来学习因果结构。
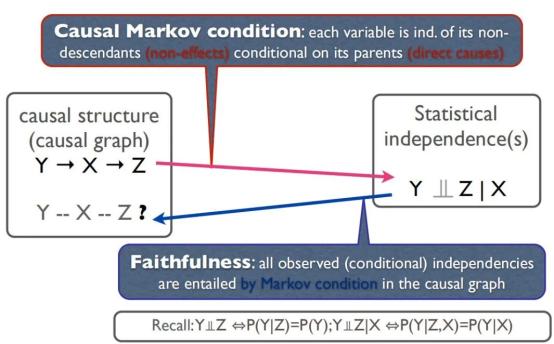
马尔可夫条件说的是任何变量,给定其父节点,都和它的非后代 (non-descendants) 统计独立。上图中给定X, Z和Y是统计独立的。马尔科夫条件提供了如下蕴含关系:结构图中表示的独立性->概率独立性, 或者等价地:概率依赖性->结构图中表示的依赖关系。值得一提的是,马尔科夫条件在一般情况下都是满足的,但在量子物理中需要更进一步的研究。
为了在因果图结构和概率独立性之间建立一个对应关系,我们不仅需要马尔科夫条件,还需要faithfulness假说。它说的是:所有观测到的概率条件独立性都包含在马尔科夫条件中。也就是它提供了如下的蕴含关系:概率独立性->结构图中表示的独立性, 或者等价地:结构图中表示的依赖关系->概率依赖性。
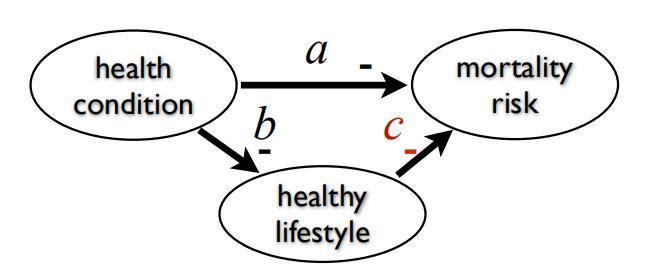
上图中,如果a=-bc,健康状况和死亡风险之间是统计独立的,因此因果关系变得无法检出。为了避免该状况,需要Faithfulness 假说,排除上述的可能性。
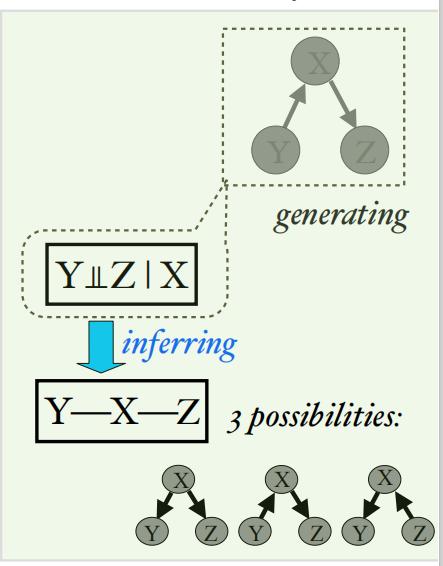
例如上图中,如果能够从数据中得到,在给定X时,变量Y和Z之间相互独立,并且其他独立性都不满足,可以据此推出在图中右下角的三种可能的因果图。在满足上述的两条假设时,可使用PC[1]算法来找到因果图。
注意使用约束的因果发现算法只能找到马尔可夫等价类,即所有边都是能唯一确定的,但某些方向不能唯一确定。特别是在只有两个变量时,这两个变量的因果方向不能以此来确定。确定任意两个变量之间的因果方向可以进一步通过下面介绍的基于功能因果模型的因果发现实现。
除了上述基于条件约束因果发现算法,另一类因果发现算法是基于功能因果模型的。在该模型中,结果Y可以表示为原因X和噪声项E的函数:Y=f(X, E),其中X和E独立。
通过合理地限制因果机制f的函数空间,我们可以发现非对称独立性,从而可以判定因果方向。即如果在正确的因果方向,通过用结果Y对原因X做回归,得到的噪声项是和X独立的。但如果反过来用X对Y做回归,得到的噪声项和Y是不独立的。
目前的研究表明当f满足以下三种条件的一种时,噪声和假设原因之间的非对称独立性满足:(1)线性非高斯模型,即Y = a*X+E;第一个能发现完整的因果图的LiNGAM模型即是基于此。(2)非线性加噪声模型:Y=f(X)+E。以及更通用的(3)后非线性模型 (post-nonlinear model) : Y = g(f(X)+E)。
现实世界中,因果图并不是一成不变的。上述方法仅适用于寻找静止的因果图,对于变化的因果图,可以通过因果机制独立变化的非对称性, 来判定因果关系的方向性[5],这是因为在大多数情况下,当因果图改变时,原因的分布和给定原因下结果变量的分布变化独立性,在错误的方向往往是不成立的,即P(cause)的变化和P(effect|cause)的变化是独立的,但P(effect)的变化和P(cause|effect)的变化是不独立的。
3. 因果发现有什么用
因果理解带来的好处已经在一些机器学习的任务中有所体现,比如迁移学习[2, 3]、非稳态数据的预测[4]、分类、聚类、强化学习等等。
迁移学习指的是要已学到数据特征的模型能够在新的场景下尽可能地被复用,通过相对较少的训练得到较好的表现。如果知道了因果模型, 就可以帮助更好地做迁移学习。我们可以更有理有据地做适应性预测,知道哪些部分发生了变化,遵从什么样的规则在变,而不是像黑盒一样盲目地做。并且用更少的数据和计算时间,即降低了样本复杂度和模型复杂度,有针对性的重新训练模型中因果关系改变的部分。
因果发现还可以简化模型,去除模型中和因果链条无关的参数,这样不仅不会影响模型的效果,还能够让模型更加具有解释性。另一个提升模型可解释的方法是识别出不同任务间改变的因果链条有哪些,从而让新模型能够更容易地迁移到新的任务。
经由因果发现,还能够更准确地在时间序列的非稳态数据上进行预测[4],下图是基于真实的美国1965-2017年间季度GDP、失业率、通胀率和经济增长率之间的时序数据,经由因果发现得出的即时的因果关系图。
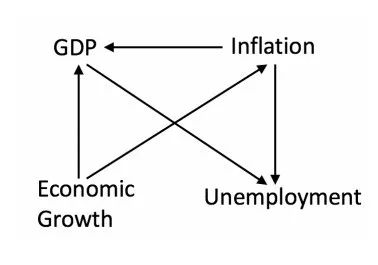
研究发现使用了因果发现的模型(比如说基于上图的因果关系),在基于过去数据对未来情况进行预测时,相比传统模型误差更小。这说明了因果发现能够用于提升模型对复杂系统的刻画精度。
4. 总结
数据分析界流传着”啤酒和尿布“的故事,说的是通过分析,发现超市中啤酒和尿布的销售量存在相关性,然而要得到这是由于买尿布的年轻爸爸会顺便买啤酒犒劳自己这一因果联系,就需要额外的信息。而唯有找到了因果联系,才能确认干预手段,即将这两个商品放在一起是有用的。
因果发现让数据分析能够在不引入先验知识的情况下,自动化地在观测数据中找到因果联系,相比传统因果推断,不需要领域知识去构建待检验的因图图,对机器学习和数据分析也都会有所助益。
学习因果发现的算法及模型,首要的是弄清楚模型的假设,模型的假设决定了其适用领域。因果发现的方法虽然很多,但通常依赖的是三种独立性,据此可以将其分为三类。
这三种独立性分别是:(1)条件独立,即在给定变量X后,变量Y和Z之间相互独立,据此可以剔除因果图中的连接;(2)噪音独立,即原因和噪音无关,因此会出现不对称性,据此确定因果链条的方向;(3)因果机制的变化独立性,即原因和给定原因的结果各自对应的分布是独立变化的,由此来在因果关系改变时,进一步确定因果方向,以及更好地进行Domain Adaptation。
参考文献:
[1] Spirtes et al., Causation, Prediction, and Search. Spring-Verlag Lectures in Statistics, 1993.
[2] Zhang, et al., Domain adaptation under target and conditional shift, ICML, 2013.
[3] Zhang, et al., Domain adaptation as a problem of inference on graphical models, arxiv 2019.
[4] Huang, et al., Causal Discovery and Forecasting in Nonstationary Environments with State-Space Models, ICML, 2019.
[5] Huang, Zhang et al.. Causal Discovery from Heterogeneous/Nonstationary Data. JMLR, 21(89), 2020.